David Simmons-Duffin @ Caltech

Honda Needs a Tune-Up

This is the story of how Honda engineers screwed up a big expensive project with a simple arithmetic mistake, tried to fudge their result with sound editing software, and congratulated themselves for being totally awesome.

When I was a kid, my family used to drive up to The Pinery in Ontario, a beautiful park by Lake Huron. Very scenic. My favorite part, though, was a stretch of road a half-hour outside of the park. To discourage reckless Canadians from barreling past the houses and barns, the local government carved five sets of grooves in the road before every stop sign. Drive over them, and the car would vibrate: “vbvbvbvb... vbvbvbvb... vbvbvbvb... vbvbvbvb... vbvbvbvb.” The faster you drive, the higher the pitch.

My Dad is a musicologist, with a particular interest in tuning. So there was no way he was going to pass up the chance to experiment with this instrument. Every time we approached some grooves, he'd start fast over the first set, and try to slow down by the last set, to play a descending scale: G-F-E-D-C. If there was no oncoming traffic after the stop sign, he'd swing over to the other side of the road and play an ascending scale as we sped up.

Ratios of speeds correspond to ratios of vibration frequencies, which correspond to intervals between notes. To play an ascending scale C-D-E-F-G, you need to drive at these ratios to your starting speed: 1 - 9/8 - 5/4 - 4/3 - 3/2 (for example, 24 - 27 - 30 - 32 - 36 mph). 1

Playing a scale with a '95 Toyota Previa is not easy. The notes tend to come out a little wonky — we'd get the half-step between E and F too wide, and with not enough space between F and G. It usually sounded kinda modal... but still awesome.

Professionals?

So imagine my delight when I heard about this musical road [CNET] that Honda built in Lancaster, CA.. A team of engineers carved some grooves into a highway that were carefully spaced to play the William Tell Overture as you drive over them at a constant speed. Awesome, right? The problem is, it's spectacularly out of tune.

Here's the original melody:

And here's the Honda road again:

The Honda version isn't simply out of tune... the notes are just wrong. The original starts with a rising 4th, F-B♭,2 and eventually reaches an octave above the starting note before descending to the tonic F-E♭-D-B♭.3 But Honda's version starts with a rising major 3rd, and its top note is a major 6th above the starting note. Some might have noticed that the last few notes in Honda's commercial sound OK. That's because they edited over them! I can prove it.

Basic melody in the William Tell Overture (schematic)

The CNET article above speculates that Honda designed the road specifically for the Honda civic driving at the speed limit, and other cars might need to drive at a different speed to make it sound better. But if you're going at a constant speed, all that matters is the spacing between grooves. Speeding up or slowing down just transposes everything. It would be theoretically possible to "correct" the melody by driving at different speeds (like on the road to the Pinery). But the notes on the musical road are too closely spaced for all but consummate musician Mario Andretti.

It also doesn't matter what car you drive.4 The vibration frequency is f = v/d, where v is the car's speed, and d is the distance over which the road pattern repeats. There's no place in the equation for wheel spacing, tire size, side-impact airbags, etc. All of these things affect the quality of the sound, but not the pitch.

So why is the musical road so unmusical?

The Error

Honda posted a series of 5 ridiculous videos: [Part 1][Part 2][Part 3][Part 4][Part 5], in which they talk about all the hard work they did and congratulate themselves for being so awesome. There are lots of complicated sounding numbers, there's a "Mathematician/Musician," and plenty of experts. I'm sure some people behind the project understood what was going on. But I think they failed to anticipate a basic misunderstanding on the part of the groove-designers.

In the fourth "making of" video, they mention that the initial note, a low F, has a spacing of 4 inches (4in) between grooves (1:47):

From the video, it looks like the grooves themselves are about 1in wide. Now, suppose you want to make the B♭ a 4th above F. A perfect 4th is a fequency ratio of 4/3, so you should multiply the width by a factor of 3/4... But the width of what?

Based on the Civic's 106.3 inch wheelbase, we can see from this picture that s+g is about 5 inches. Honda says the lowest note has a 4 inch spacing, so that's consistent with 1 inch grooves.

The width that really matters is the total width of the spacing plus groove (s+g). That's the distance over which the road pattern repeats, so that's the distance over which the car completes one vibration.5 Suppose you didn't know this, and only changed the spacing, from s = 4in to s' = 3/4 × 4in = 3in. Then the frequency ratio is (s+g)/(s'+g) = (4+1)/(3+1) = 5/4, a major 3rd, not a perfect 4th. What about the octave above the starting note? An octave is a frequency ratio of 2/1, but if you only changed the spacing to s' = 1/2 × 4in = 2in, you'd get an actual ratio of (s+g)/(s'+g) = (4+1)/(2+1) = 5/3, a major 6th, not an octave.

Oops.

making an octave, incorrectly

There are two ways you could correct this problem:

  1. Adjust the groove width g as well as the spacing s. For instance, to make an octave, use a spacing s' = 2in and a groove g' = .5in, giving a fequency ratio (s+g)/(s'+g') = 5/2.5 = 2/1. This is probably hard with typical cutting tools. Also, the engineers may have found that they need to make the grooves bigger than some minimum width to get a good sound. So on to method 2...
  2. Over-adjust the groove spacing so that the total g+s is correct. For instance, to make an octave, adjust the groove spacing to s' = 1.5in, so you get a frequency ratio of (s+g)/(s'+g) = 5/2.5 = 2/1.

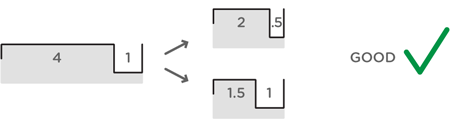making an octave, correctly

The Coverup

Armed with this theory for why the musical road sounds so bad, I crunched some numbers in Mathematica, and was able to reproduce Honda's result, sort of...

Here's Mathematica playing the correct William Tell Overture:

And here's Mathematica programmed to make the mistake I think Honda's engineers made:

And here's honda's commercial version again:

Notice that a few notes in the commercial sound different from Mathematica's version. Particularly at the end. Honda's last few notes are sort of... in tune! Turns out that's a bit of Hollywood magic. Here's a recording I stole from a different video of someone driving down the Musical Road:6

What happened to the ending? It's all funky again. Go back and listen to the Mathematica version that mimics Honda's mistake. Same funky ending.7 Whoever put together the Honda commercial must have edited over the ending, assuming that as long as the last few notes were correct, no one would notice anything wrong.8

What I don't understand is: if they were going to doctor the sound, why didn't they just correct the whole thing? It's not that hard. My dad did this version in about 20 minutes:

Aftermath

I learned something else kind of ridiculous from this analysis: if Honda didn't doctor the overall pitch of the melody in their commercial, then they were speeding. The opening frequency is about 238Hz, which corresponds to a speed of about 67mph if the road pattern repeats over 5in. But they mention in one of the videos that the speed limit is 55! Crap.

In fact, in this youtube video, where they explicitly state they're going 55mph, the melody starts a minor third below the Honda commercial. A minor third is a frequency ratio of 6/5, so this is consistent with Honda's driver doing 6/5 × 55mph = more than 10mph over the speed limit...

Another funny point is that some of the intervals you get from Honda's miscalculation are pretty bizarre. The D, a major 6th above the starting F, should have a frequency ratio of 5/3 above the starting frequency. Instead, it has a ratio 5/(4 × 3/5+1) = 25/17. This isn't really in the western scale. It's about 2/3rds of the way between an augmented 4th and a pure 5th. Microtonal composers like Easley Blackwood might have found a use for it, but I don't think it's what Honda was after.

If I were them, I'd seriously consider paving over the road. In fact, it seems like some local residents might do it for them. There is another option, though. If they bring in the bulldozers, and shuffle around a few chunks of asphalt at the end of the road, they might get a decent rendition of "When The Saints Go Marching In."

Update [12/30/08]: Added picture comparing grooves to Civic wheelbase

Update [5/2/11]: I am both sorry and delighted to hear that they rebuilt the musical road (see, e.g., here), and they fixed nothing. Here it is on April 28, 2011:

Just... wow.

Update [4/15/18]: This post was recently featured on Tom Scott's Youtube Channel "Amazing Places." As of today, the video currently has about 5 million views. It was also mentioned in The New York Times.

  1. If anyone's wondering what happened to the 1/12th powers of 2 in this whole tuning discussion, I'm using what's called Just Intonation, which is an (often better-sounding) approximation to the Equal Temperament system most people know. Actually, it's really the other way around: the reason we use 12 equal semitones is that it lets us approximate nice integer ratios like 3/2, 4/3, 5/4, etc.. This is a long story that I'm not going to get into here.
  2. Actually, the starting note in the recording is around a B♭. I'm going to pretend like everything is in the key of B♭ (so the starting note is F), since that's the key they talk about in the making-of videos. a picture of Honda's score a picture of Honda's score Sorry to the perfect-pitch people.
  3. The original melody actually has a run down to the B♭: F-E♭-D-C-B♭. Honda apparently decided this was too complicated and used a simplified version. That's what I'll stick to here.
  4. With one exception that can't fix the tuning. See my comment, below.
  5. More precisely, once you know the force driving the vibrations is periodic with period T=d/v, it follows that the vibrations themselves have that periodicity, so the Fourier transform of any resultant sound is only nonzero at integer multiples of f=1/T. For more explanation, see the second comment, below.
  6. I've actually transposed it up to be in approximately the same key as the other recordings in this article. By the way, there are hundreds of such videos on Youtube.
  7. Aside from a single passing note. If I change the closing notes from F-E♭-D-B♭-D-B♭ to F-E♮-D-B♭-D-B♭, and apply the Honda miscalculation, it sounds almost exactly like the undoctored recording of the musical road. So it appears that there are two errors at work here: the groove spacing miscalculation, and replacing an E♭ with an E♮.
  8. It seems like Honda fixed up some of the other notes, too, to get a more pleasant sound. Some might object that it's easy to make the notes sound bad by speeding up or slowing down as you drive down the road. However, I don't hear anything like that in the random person's recording. The melody returns to previous notes with reasonable accuracy, which it wouldn't do if the speed were varying.

Comments

  1. Jeremy HeilmanDec 24 2008 11:27:07

    Brilliant work, David. I must have just come home from church choir practice when I first heard this commercial, because I recall shouting at the TV, "You think YOU have tuning problems...."

    In addition to your point that it is the total period (space + gap) that determines the pitch, the ratio of space/gap will alter the overtone series and the timbre of the road. For instance, if the gap and space were always equal (and half the total), the overtone series would be that of a square wave (given by a Fourier series http://www.numerit.com/samples/fours/doc.htm) with the loudest components grouped near the fundamental. I would think this would be the best reflection of most instruments you could get from a road (but likely still pretty poor). However, using a big space and a little gap (or vice-versa) would result in many of the highest frequency harmonics having large amplitudes, for a "tinny" sound. If anyone has ever driven a Civic, they know it sounds pretty tinny already, and doesn't need any help from man-made potholes!

    The other gross oversight (this would have actually gotten them some major awesome points in my book) would be to cut the grooves on a diagonal, such that no two tires are in the same point with respect to the pattern at the same time. Then, each tire would sound individually, and you would have a rubber quartet playing in unison. Or cut half the pattern on the left side of the road and half on the right, to make diads!

    Of course, I think if the music you make sounds worse than the beginning band, you'd be better of selling insurance.

  2. davidsdDec 24 2008 16:50:27

    @Jeremy:

    Some good ideas! I can't imagine what counterpoint would have sounded like if they didn't get a single melody straight...

    Some people have asked me about something that you touch on in your comment, so I thought I'd answer it here. There is a way that the kind of car can affect the pitch: the periodicity of the road guarantees that only integer multiples (called "harmonics") of the fundamental frequency f=v/d can appear. The relative strength of these harmonics determines the quality or timbre of the sound, and it can depend on what shape the grooves are, the distance between the front and back wheels, etc.

    An extreme case of this (as my friend Matt points out) is that the fundamental frequency f can be suppressed or even disappear. For instance, if the wheel spacing is a half-integer times the groove distance d=s+g, the road would vibrate the car at twice the rate, and it's possible that the frequency 2f would be stronger than the fundamental (though I think it's unlikely the fundamental would disappear entirely).

    This would make the melody jump up by an octave whenever it hit a certain note. This doesn't happen in any of the recordings I've heard (the full range of the melody is only a major 6th), so it's fair to say that this effect wasn't part of Honda's design. The key point, though, is that the periodicity of the road guarantees that this is the only way that the make of the car can affect the sound, and it doesn't happen in practice (nor could it fix the tuning at all).

  3. DadDec 24 2008 21:01:30

    Great post, and interesting comments about the possibility of an upper octave being heard if the wheelbase is some odd multiple of 2.5in.

    As it happens, the 2008 Honda Civic does not fall into that category, having a wheelbase of 106.3in for the sedan, and 104.3 for the coupe. There are some cars where it could apply, however: the new VW Tiguan has a "unique" wheelbase of 102.5in, and the 2007 Aveo has a wheelbase of 97.5in.

    That could affect the sound of the lowest (i.e., first) note, but other wheelbase lengths could affect other notes, could they not? Since the proportions used by Honda for this project are not simple ratios for s+g, it would take some investigating to see what works on the road. Anyone out in California with a Tiguan or an Aveo for starters?

    Come to think of it, this would only work for longer notes, I think -- longer than the wheelbase, at least. If the note only covers, say, 8ft of road, it would simply extend the fundamental pitch by having the back wheels vibrate after the front ones were done.

  4. Paul RapoportDec 25 2008 16:43:38

    This is,in the words of a former high school music teacher, a ruddy riot. (He said that when we squawked in a Honda tuning or an unreasonable facsimile thereof.)

    Reasonable that you consider a major scale to have a 9/8 major second. I'm sure you're aware of the "second scale degree" problem, its not being justly in tune with both the 3/2 and the 5/3, and the proliferation of issues arising from that.

    I like that you arrived one place at a 25/17. At 667.67 cents, it's about 2/3 the way between certain intervals, as you said, but I imagine there you're thinking in 12-tone equal. It's a different distance (about 3/5) if you take the just augmented 4th of 10/7. All of which affects your point not a bit.

    As for Easley Blackwood's interest in a 25/17, you'll find something very close in his 18-tone ET etude. But he's never taken a compositional interest in just tunings. Ben Johnston, on the other hand, has written music with harmonics up to 32. Whether there's a 25/17 anywhere, I have no idea.

    Thank you once again for your lesson in Civics. Beats the usual kind. Do you think Honda's version is any better if it's painted in blues?

  5. Mano SinghamDec 29 2008 17:44:26

    David,

    Very interesting post! It reminded me of something I was told a long time ago but which I never tried to verify.

    You know those rumble strips by the side of a highway that warn you when you are drifting off the road, say if the driver drifted off to sleep? I was told that engineers once designed them so that they would say something like "Wake up!" but found that on testing, it gave drivers such a shock to hear a disembodied voice that they abandoned the plan.

    I suspect that this story is too good to be true but was curious if you had encountered anything like it in your research on this.

  6. davidsdDec 31 2008 05:31:23

    @Mano:

    I can't seem to find anything about rumble strip voices, but I did come across this video about a musical road in South Korea that was apparently created to keep drivers from falling asleep (unlike the one in Lancaster, CA which was mostly an advertising stunt).

  7. Robert KMar 6 2009 00:16:53

    After seeing the TV ad I was literally furious that Honda had made a self-congratulatory commercial about a project that had so obviously failed. So I Googled it, but no one seemed to have noticed that the melody was totally wrong. I thought maybe I was going crazy. The worst part was that the math behind designing it should've been so simple, I couldn't understand how they could've screwed it up.

    I just wanted to thank you for posting this and for doing the analysis to confirm what went wrong, although I'm still amazed that they could have made this mistake. I don't even really know what this blog is about, but I had to express my gratitude. It's good to know that someone else noticed.

  8. davidsdMar 26 2009 20:19:52

    @Ben, Thanks! That is awesome about the cheese.

  9. BenMar 26 2009 19:57:09

    Fantastic. I want to second exactly what Robert K said (boy, did I think I was going crazy!). So nice to know that there's an explanation for what went wrong. As a footnote, I used to sell blue cheese to Easley Blackwood on a surprisingly regular basis.

  10. PJApr 19 2009 01:51:21

    Thank you! I needed to find some meaning or justice behind the trashing of the William Tell melody. If they didn't get this right, what does this say about their newest cars?

  11. NickApr 1 2009 18:40:38

    I'm so glad that this bothered someone else as much as it did me.

  12. ElliottApr 19 2009 16:03:22

    David - In the early 90's Tim Sprunger who worked at Walt Disney World at the time, built a musical road as a demo project that Disney never picked up on. He's an artist/musician and went through all the same calculations you list above. His road played Zip-py-do-da of course and has a video of the testing. His design used raised ridges made of a special aggregate and epoxy formula. He found, unless the grooves were made in concrete the summer Florida heat would soften the asphalt and almost erase the grooves in one summer. Tim lives Kissimmee FL

  13. JohnApr 18 2009 22:06:17

    Amazing analysis, David. Add my name to the list of people who had NO idea what the original Civic-produced ditty from the commercial was supposed to represent. I didn't even think William Tell Overture until I read it here. What a joke. In hindsight, I particularly like the college kids in the commercial cheering in celebration of several months spent producing a song which sounds absolutely nothing like the original.

    Remember kids, reality is what the man on the TV told you. That is EXACTLY how William Tell is meant to sound, because the faux-college kids from Honda Advertising TOLD you so. hahaha

  14. davidsdApr 19 2009 17:28:04

    @Nosmo, That's a good idea -- they definitely could have used something like that during the editing process. They certainly made sure each pitch in the commercial is a note on the piano (as opposed to the way it really sounds, which has funny microtones you can't play on a keyboard). But I'm not sure they always modified the pitch to the nearest note. For example, at the end, the honda commercial goes B♭-D-B♭, but I think the nearest notes would be A-C-A. Sounds like they were being a little more liberal with the pitch doctoring.

    @Elliott, very interesting! I do remember reading something about asphalt being a difficult "medium" in hot climates. That's cool that Tim figured out a solution. I wonder if the city of Lancaster (which apparently has rebuilt the William Tell road as a tourist attraction) is aware of this.

    Everyone, thanks for the kind words! I totally agree that it's ridiculous that Honda is high-fiving themselves on every channel for such an obvious fail. It really doesn't sound anything like William Tell. I like Zach's original thought that Honda's engineers were just a bunch of indie rock lovers :). PJ, I hope this writeup provides some form of justice. Boy, does Honda deserve it.

  15. ZachApr 16 2009 00:36:46

    Excellent write up. I searched for an explanation to the screw up and found this site. The commercial always frustrated me because it did not makes sense why Honda would choose a song that was not commonly recognizable. I figured maybe the engineers were a bunch of indie rock lovers and picked some obscure cult song (p.s. i like indie rock). It wasn't until about the 10th time hearing the commercial that I recognized the tempo of the song they were apparently trying for. This engineering screw up clearly is not something they should be marketing at all let a lone during every commercial break on every channel.

  16. NosmoApr 10 2009 12:19:28

    A coworker commented that there must be some sort of software that corrects pitch, and it could be that the correction they did was run the sound through that software and it just changed the frequencies to the nearest note? That may explain why the correction they did was not done properly. Does this make any sense?

  17. AdamApr 15 2009 01:35:06

    I'm glad I found this. Only after watching that advert about ten times did I even figure out that it was William Tell. It sounded nothing like it until I used some imagination.

  18. coreopsisApr 14 2009 19:30:48

    Awesome analysis! Someone should have paid you to write this article.

  19. GooberliciousApr 21 2009 10:29:42

    As a Lancaster resident, I had to try it. It was in the Western part of the Antelope Valley (1 hr north of LA in the high desert) on Avenue K between 60th and 70th Streets West. So I drive over the grooves and found that I couldn't make head or tail of what it was! I'm sort of a musician (been piano-ing for 31 years) and thought, "OK, cool, now what was that?" Due to some cranky residents in the area and nut-job drivers, they have since removed the grooves and moved them to Avenue G between 30th and 50th Streets West, which is conventiently on my way home from work. I decided to drive the speed limit (55) and try it again and again. The new grooves sound even WORSE! I thought maybe it was my speed understanding frequency changes with speed in this case. Being the good enginerd that I am, I decided to experiment with differing speeds, at 1 mph increments. To no avail. A colleague of mine sent me this link and now I have my answer. It's all mucked up!!!!

  20. KentonMay 29 2009 02:34:43

    I hope the congratulations aren't getting old - I just wanted to echo the same sentiments expressed above. I live in Canada and just started seeing this ad online thanks to a proxy server that allows me to watch American programs. It took two listens for me to get fed up and track this down on Google.

    I still can't believe the final ad in the series where the engineers high-five after listening to a clearly failed attempt - even worse when you consider they were hearing the "pre-re-tuned" version in the car as they congratulated each other. But I'm sure they took a gamble that the vast majority of people wouldn't notice, and judging by the lack of search results on Google, I'd say they gambled right.

    Either way, your time on this was appreciated. It's always nice to know your part of a crowd, even if it is small. ;)

  21. WilliamMay 14 2009 17:45:14

    Brilliant analysis. Win for David, his think-outside-the-box dad, and the world at large. I really enjoyed the musical comparisons. I don't know anything about notes or stuff like that, but I can certainly appreciate a good and scientific presentation.

    Thank you.

  22. ChrisJul 22 2009 02:25:15

    that was really interesting. when i first saw the commercial i had no idea what melody they were trying to play with the car... it sounded like they just made it up

  23. Trevor CoxMar 1 2010 11:51:49

    This is a great post and I've just used it on Sonic Wonders, my new website about Sound Tourism.

  24. PeterSep 16 2010 07:53:58

    Bravo! Terrific analysis. Must have been thrilling to find that the numbers and pitches worked out when you predicted their mistake.

    Too bad Honda got filched by the people they contracted. The whole concept is a cool idea--hopefully someone else will do it better... and maybe include a longer and more interesting melody.

  25. Honda Needs a Tune-Up | Maszman Speaks!Jan 6 2011 09:11:13

    [...] I’m sure you’ve seen the Honda com­mer­cial where they cut grooves in a road so that a Honda Civic plays a tune when it dri­ves over it at 55 mph. What you might not real­ize is that Honda made a mis­take in cut­ting the grooves and edited the audio to make it sound sort of cor­r.... [...]

  26. David EdwardsMay 10 2011 00:13:42

    Hi David.

    Jeremy Heilman raised the idea of using diagonal grooves, or cutting different grooves for each side of the car. That could be tried on the existing road, by using a Renault 16 as the test car. This had two wheelbases which differed by 2.76 inches, so you would get a different effect from each side - kind of like driving at two different speeds at the same time.

    Wikipedia has an article about this car; http://en.wikipedia.org/wiki/Renault_16

    David Edwards

  27. Mike J.Aug 21 2011 03:39:51

    Late to the party but unfazed...

    How come the tire manufacturers haven't caught on? Your tires could play a wake-up message at all times! My tires already have a distinct growl on hard turns, too, which could be adapted into a critical warning.

    On the other hand, the reduction in crashes from drivers falling asleep might be offset by the number of intentional ditchings by drivers driven to insanity by the same three notes over and over and over and over.

  28. Larry WiniarskiAug 4 2012 07:06:54

    Ugh...

    It's obviously not the William Tell overture. Maybe it's the "Will you promise not to Tell overture"

  29. Trevor CoxNov 18 2012 05:09:15

    I visited the re-made road in Lancaster last summer which is badly out of tune as well, if anything the high note is even flatter than the original. I took along a tape measure and an audio recorder as well. I drove at at about 60 mph using cruise control to maintain constant speed.

    The grooves are 1”.

    For the lowest note there is a spacing of 3.846” between groves, making a distance between identical parts on the rumble strip 4.846”. This gave me 217 Hz, a note just below A3.

    For the highest note of the melody the frequency was 333 Hz (closest note E4) when it should be an octave higher than the lowest note (434 Hz, A4). The distance between identical parts of the rumble strip was 3.152” when it should have been 2.423”.

    It seems that they didn't half the spacing between the grooves, and if they had done that it would have been less flat (but still awful).

    Trevor

  30. Dave ScheivertOct 7 2014 01:19:11

    David, seems to me you just have to change the notes that put this in a Minor key, and it would be passable. (and not make me crazy IF I have to drive over it)

  31. PooriyaApr 28 2015 11:35:58

    Hi, my name is pooriya and im trying to build amusical road in my country. I live in iran and my equipments are low, i actually cut grooves of 12,6 mm in width and depth with a 12 mm spacing and another 24,12mm in width snd depth with 24 mm spacing grooves on the ground but when i go over them its mute ,there is no sound . And i dont know why! Tell me whats wrong please help me thanks

  32. davidsdApr 28 2015 12:10:52

    Hi Pooriya, What a great project! My guess is that your grooves might not be spaced far enough apart from each other. You want to make sure that when wheels pass over the grooves, they oscillate up and down a little bit. If the grooves are too close to each other, and the wheels are big, then the wheels won't be able to tell the difference between them. So my suggestion is to try making the grooves farther apart. (Note that this means you'll have to move faster over them to make the same sound.) 12mm sounds like a reasonable depth. But I'm not an expert, so you'll have to experiment!

  33. PooriyaJun 14 2015 06:56:14

    Hi david thanks for the advice. But i have a major problem with what you basicly say here and that is based on my experiment which i cut grooves of 24,12 mm in width and depth with 36 mm spacing and 48,12 mm in width and depth with 72 mm spacing and another 24,12 mm in width and depth with 96 mm spacing then used sensors to determine the frequencies and found out that the frequencies does not depend on the spacings becuase the first and last grooves which are the same in width but have diffrent spacings, had the same frequencies at a given speed! And i think its the way it should be because we have two frequencies here one is the impact of the tire and the groove which i think should determin the note and the second frequency is the repeatition of the first. To better understand this you can think of a sound of a fork hitting on a table, that has a specific frequency but reapeting it could be 10 times per secon witch is a frequncy but doesnt determins the note am i wrong??